[コンプリート！] 1次式の計算の仕方 432046

中２数学 式の計算 １３ 中学数学高校数学個別指導in山形市 数専ゼミ

まずは、xの値を1刻みで入力していきます。 続いて、一次関数のyの値を求めていきます。 セルに＝5*（xのセル）2と入れます。 Enterキーで一次関数の計算を確定させていきます。 オートフィル機能の意味と使い方 （セルの右下にカーソルを合わせた際に例 1 多項式 P(x)=x 2 x3 を1次式 x−1 で割る計算は右のようになるが、このときの余りは P(x) の x に 1 を代入するだけで求めることができる。 P(1)=1 2 13=5 2 多項式 P(x)=x 2 −3x4 を1次式 x2 で割る計算は右のようになるが、このときの余りは P(x) の x に −2 を代入するだけで求めること

1次式の計算の仕方

1次式の計算の仕方-定義 対数は次のように定義され、記号 log を用いて表されます。 M = ap (a ≠ 1, a > 0, M > 0) M = a p ( a ≠ 1, a > 0, M > 0) という関係があるとき、 p p を a a を底（てい）とする M M の対数といい、 p = loga M p = log a ⁡ M と表す。 M M を 対数 p p の真数という。 この1次式の分数の計算中1数学 1次式の分数の計算中1数学 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try

中学1年数学 文字と式 1次式の計算 加法 減法 乗法 除法 Youtube

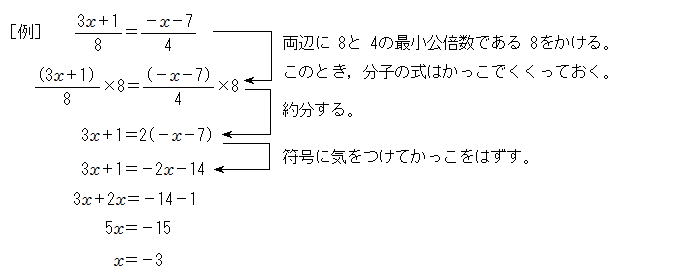
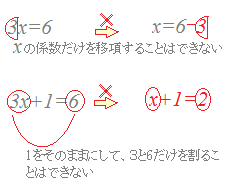
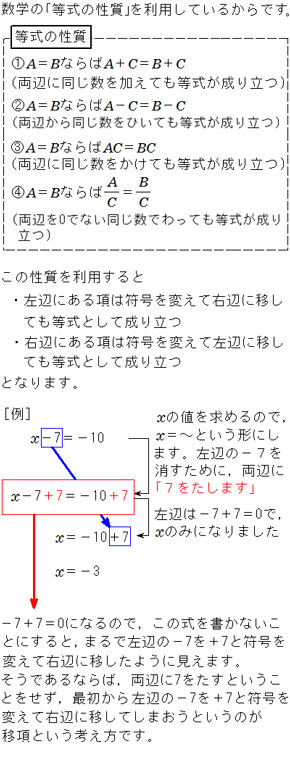
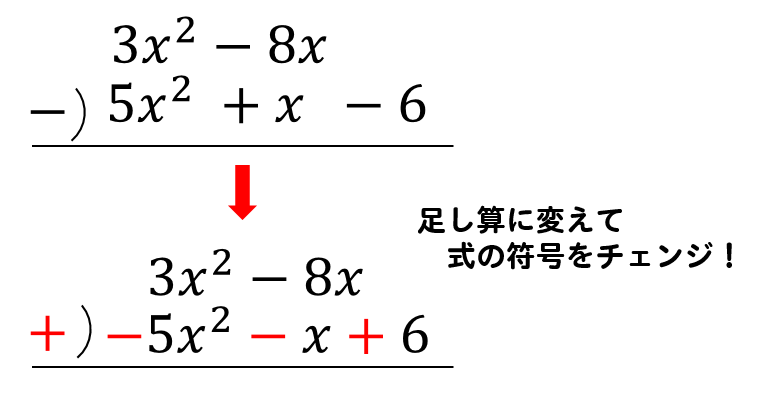
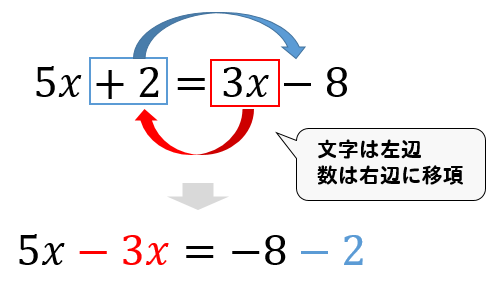
この場合には両辺に×(－1)をすることによって、今後の計算を少し楽にしてやることができます。 ④ x の前についている数で両辺をわる。 最後は x の前についている数で両辺を割ります。ねらい： 項が2つの1次式と1次式の加法と 減法の計算の仕方を理解する。 まとめ： 項が2つの1次式どうしの加法と減 法の計算は、加法は、それぞれの項を そのまま加え、減法は、ひく方の式の 1つ1つの項をひくと考えればよい。 1次式より2次式の方が，2次式より3次式の方が フィッティングが良いのは当たり前 なので，このように改良したい気持ちはよく分かります！ シンデレラフィットではありませんが（笑），キレイにフィッティングできると気持ちいいですよね！

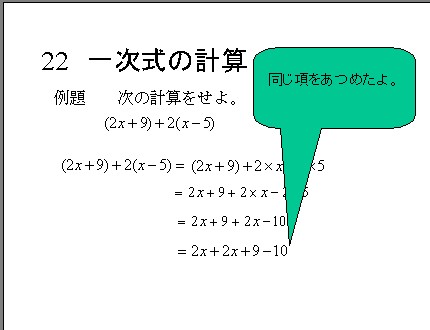
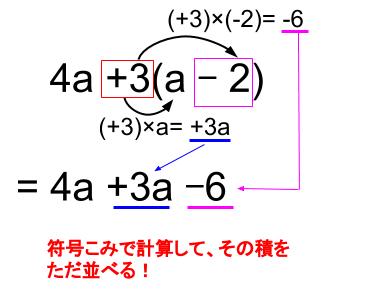
1次式の計算 一般的な1次式の計算の仕方について学習します。 分数を含む1次式の計算 分数を含む1次式の計算の仕方について学習します。 1次式2x、5yのように、文字が1つだけの項を1次の項といいます。 1次の項だけか、1次の項と数の項の和で表される式を1次式といいます。 計算の仕方 文字の部分が同じ項をまとめます。 1次式の加法・減法は、かっこをはずして分配法則をつかいます。 ※加法は、そのままかっこをはずしますが。 減法はひく方の式の各項の符号を変えてかっこをはずします そして、1次の項のみ、または1次の項と数との和で表さられる式を 1次式 といいます。 文字式の計算 加法(足し算) まずは足し算のやり方からです。

1次式の計算の仕方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

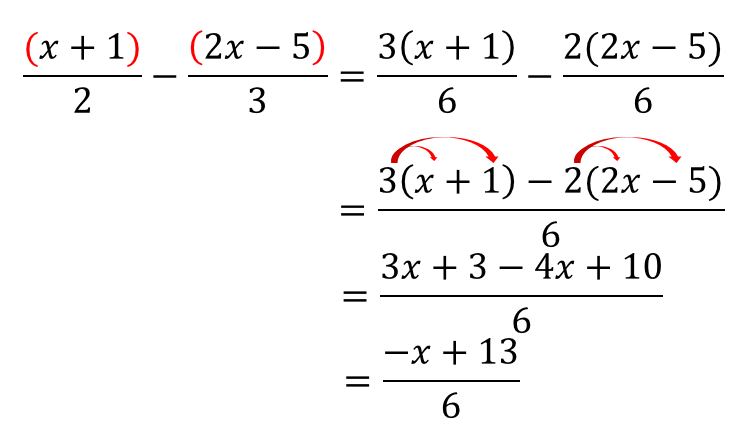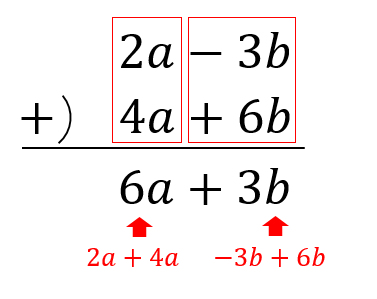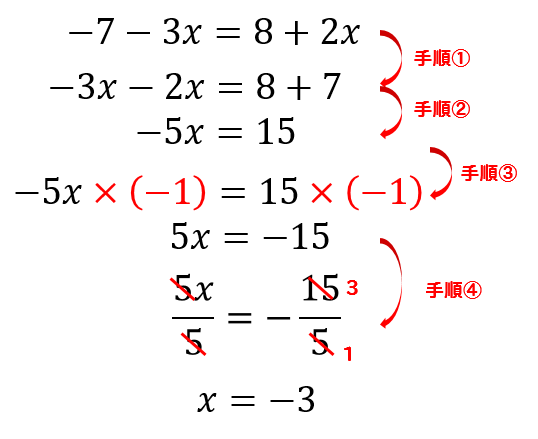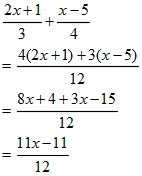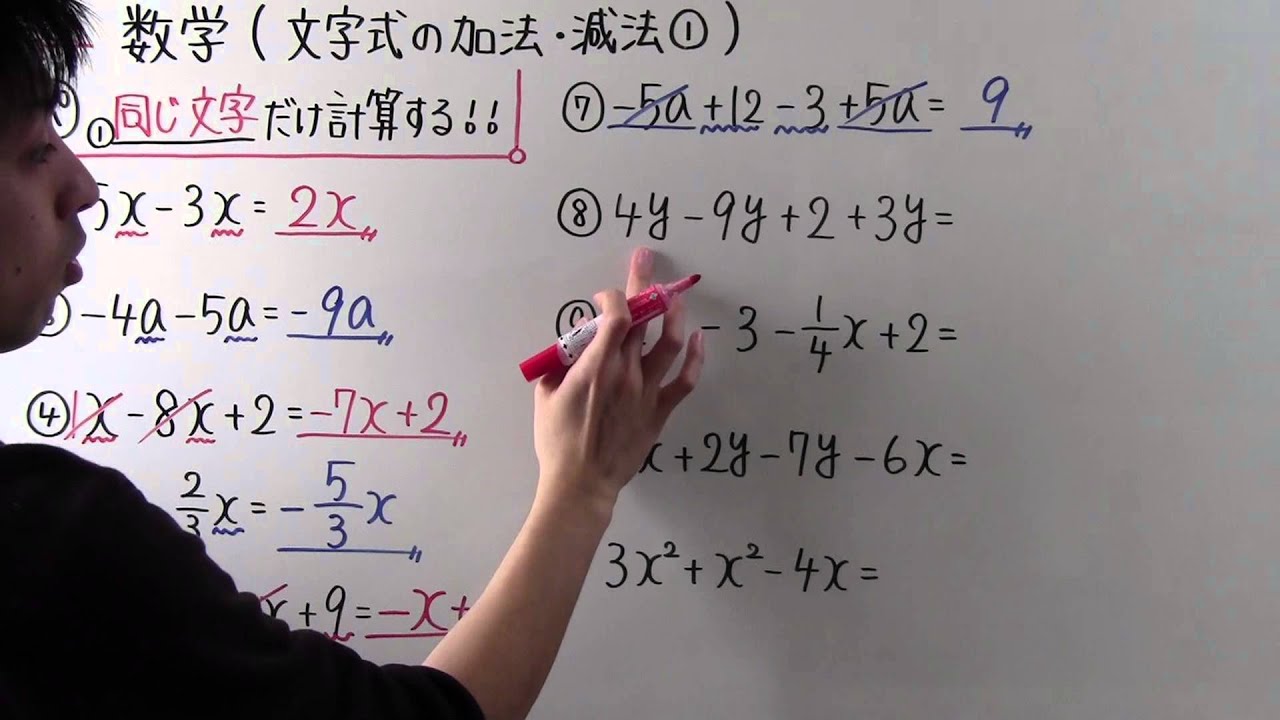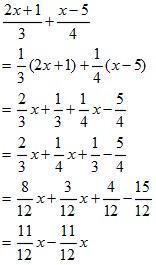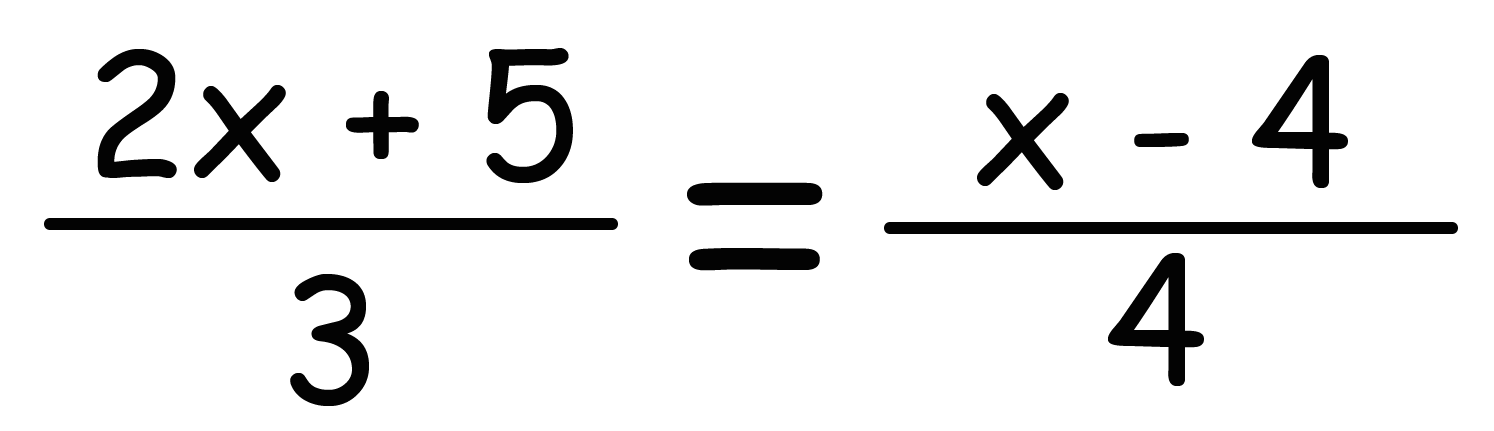「1次式の計算の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。

(a) 一般に，分数関数は（分子）÷（分母）の割り算によって商と余りに分けると，「分子の次数＜分母の次数の形」 （数研の参考書で「分数式は富士の山」と呼ばれるもの） に変形することができる．この変形により，分数関数の不定積分を求めるときは，分子の次数が分母の次数よりも低い形だけを考えればよいことになる．1次式の計算（5） ・ 文字を用いた式の計算も数の計算と同じようにみて計算の方 法を考えることができる。 ・ 1次式と数の乗法・除法，1次式どうしの加法・減法の計算 ができる。 ノート 行動観察 発表 六 3章のまとめと問 題（2）